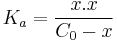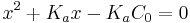Buffer solution
| Acids and Bases |
|---|
| Acid dissociation constant Acid-base extraction Acid–base reaction Acid–base titration Dissociation constant Acidity function Buffer solutions pH Proton affinity Self-ionization of water |
| Acid types |
| Brønsted · Lewis · Mineral Organic · Strong Superacids · Weak |
| Base types |
| Brønsted · Lewis · Organic Strong · Superbases Non-nucleophilic · Weak |
- For an individual weak acid or weak base component, see Buffering agent. For uses not related to acid-base chemistry, see Buffer (disambiguation).
A buffer solution is an aqueous solution consisting of a mixture of a weak acid and its conjugate base or a weak base and its conjugate acid. It has the property that the pH of the solution changes very little when a small amount of strong acid or base is added to it. Buffer solutions are used as a means of keeping pH at a nearly constant value in a wide variety of chemical applications. Many life forms thrive only in a relatively small pH range; an example of a buffer solution is blood.
Contents |
Principles of Buffering
Buffer solutions achieve their resistance to pH change because of the presence of an equilibrium between the acid HA and its conjugate base A-.
- HA H+ + A-
When some strong acid is added to an equilibrium mixture of the weak acid and its conjugate base, the equilibrium is shifted to the left, in accordance with Le Chatelier's principle. Because of this, the hydrogen ion concentration increases by less than the amount expected for the quantity of strong acid added. Similarly, if strong alkali is added to the mixture the hydrogen ion concentration decreases by less than the amount expected for the quantity of alkali added.
The effect is illustrated by the simulated titration of a weak acid with pKa = 4.7. The relative concentration of undissociated acid is shown in blue and of its conjugate base in red. The pH changes relatively slowly in the buffer region, pH = pKa ± 1, centered at pH = 4.7 where [HA] = [A-], but once the acid is more than 95% deprotonated the pH rises much more rapidly.
Buffer capacity
Buffer capacity, β, is a quantitative measure of the resistance of a buffer solution to pH change on addition of hydroxide ions. It can be defined as follows.
where dn is an infinitesimal amount of added base and d(p[H+]) is the resulting infinitesimal change in the cologarithm of the hydrogen ion concentration. With this definition the buffer capacity of a weak acid, with a dissociation constant Ka, can be expressed as
where CA is the analytical concentration of the acid.[1] pH is approximately equal to -log10[H+].
There are three regions of high buffer capacity.
- At very low p[H+] the first term predominates and β increases in proportion to the hydrogen ion concentration. This is independent of the presence or absence of buffering agents and applies to all solvents.
- In the region p[H+] = pKa ± 2 the second term becomes important and β rises to a maximum at p[H+] = pKa. Buffer capacity is proportional to the concentration of the buffering agent, CA, so dilute solutions have little buffer capacity. It is also proportional to the acid dissociation constant, Ka (not pKa); the weaker the acid the greater its buffering capacity.
- At very high p[H+] the third term predominates and β increases in proportion to the hydroxide ion concentration. This is due to the self-ionization of water and is independent of the presence or absence of buffering agents.
Calculating buffer pH (monoprotic acid)
First write down the equilibrium expression.
- HA A- + H+
The initial, change and equilibrium concentrations of these three components can be organized in an ICE table.
-
ICE table for a monoprotic acid [HA] [A-] [H+] I C0 0 0 C -x x x E C0-x x x
The first row, labelled I, lists the initial conditions: the concentration of acid is C0, initially undissociated, so the concentrations of A- and H+ are zero. The second row, labelled C for change, specifies the changes that occur when the acid dissociates. The acid concentration decreases by an amount -x and the concentrations of A- and H+ both increase by an amount +x. This follows from the equilibrium expression. The third row, labelled E for equilibrium concentrations, adds together the first two rows and shows the concentrations at equilibrium.
To find x, use the formula for the equilibrium constant:
Substitute the concentrations with the values found in the last row of the ICE table:
Simplify to:
With specific values for C0 and Ka this equation can be solved for x. Assuming that pH = -log10[H+] the pH can be calculated as pH = -log10x.
Note. When a pH meter is calibrated using known buffers, the reading gives the hydrogen ion activity rather than its concentration. In this case the meter reading may differ from the value calculated as above. For example, calculation of pH of phosphate-buffered saline would give the value of 7.96, whereas the meter reading would be 7.4. The discrepancy arises when the acid dissociation constant value is specified as a concentration quotient and would not occur if Ka were specified as a quotient of activities.
Calculating buffer pH (polyprotic acid)
Polyprotic acids are acids that can lose more than one proton. The constant for dissociation of the first proton may be denoted as Ka1 and the constants for dissociation of successive protons as Ka2, etc. Citric acid, H3A, is an example of a polyprotic acid as it can lose three protons.
-
equilibrium pKa value H3A H2A− + H+ pKa1 = 3.13 H2A− HA2− + H+ pKa2 = 4.76 HA2− A3− + H+ pKa3 = 6.40
When the difference between successive pK values is less than about three there is overlap between the pH range of existence of the species in equilibrium. The smaller the difference, the more the overlap. In the case of citric acid, the overlap is extensive and solutions of citric acid are buffered over the whole range of pH 2.5 to 7.5. Calculation of the pH of a particular mixture requires a speciation calculation to be performed.
Applications
Buffer solutions are necessary to keep the correct pH for enzymes in many organisms to work. Many enzymes work only under very precise conditions; if the pH moves outside of a narrow range, the enzymes slow or stop working and can denature. In many cases denaturation can permanently disable their catalytic activity.[2] A buffer of carbonic acid (H2CO3) and bicarbonate (HCO3−) is present in blood plasma, to maintain a pH between 7.35 and 7.45.
Industrially, buffer solutions are used in fermentation processes and in setting the correct conditions for dyes used in colouring fabrics. They are also used in chemical analysis[1] and calibration of pH meters.
The majority of biological samples that are used in research are made in buffers, especially phosphate buffered saline (PBS) at pH 7.4.
Useful buffer mixtures
-
Components pH range HCl, Sodium citrate 1 - 5 Citric acid, Sodium citrate 2.5 - 5.6 Acetic acid, Sodium acetate 3.7 - 5.6 K2HPO4, KH2PO4 5.8 - 8 Na2HPO4, NaH2PO4 6 - 7.5 CHES 8.6–10 Borax, Sodium hydroxide 9.2 - 11
"Universal" buffer mixtures
By combining substances with pKa values differing by only two or less and adjusting the pH ,a wide-range of buffers can be obtained. Citric acid is a useful component of a buffer mixture because it has three pKa values, separated by less than two. The buffer range can be extended by adding other buffering agents. The following two-component mixtures (McIlvaine's buffer solutions have a buffer range of pH 3 to 8.[3]
-
0.2M Na2HPO4 /mL 0.1M Citric Acid /mL pH... 20.55 79.45 3.0 38.55 61.45 4.0 51.50 48.50 5.0 63.15 36.85 6.0 82.35 17.65 7.0 97.25 2.75 8.0
A mixture containing citric acid, potassium dihydrogen phosphate, boric acid, and diethyl barbituric acid can be made to cover the pH range 2.6 to 12.[4]
Other universal buffers are Carmody buffer and Britton-Robinson buffer, developed in 1931.
Common buffer compounds used in biology
| Common Name | pKa at 25 °C |
Buffer Range | Temp Effect dpH/dT in (1/K) ** |
Mol. Weight |
Full Compound Name |
|---|---|---|---|---|---|
| TAPS | 8.43 | 7.7–9.1 | −0.018 | 243.3 | 3-{[tris(hydroxymethyl)methyl]amino}propanesulfonic acid |
| Bicine | 8.35 | 7.6–9.0 | −0.018 | 163.2 | N,N-bis(2-hydroxyethyl)glycine |
| Tris | 8.06 | 7.5–9.0 | −0.028 | 121.14 | tris(hydroxymethyl)methylamine |
| Tricine | 8.05 | 7.4–8.8 | −0.021 | 179.2 | N-tris(hydroxymethyl)methylglycine |
| TAPSO | 7.635 | 7.0-8.2 | 259.3 | 3-[N-Tris(hydroxymethyl)methylamino]-2-hydroxypropanesulfonic Acid | |
| HEPES | 7.48 | 6.8–8.2 | −0.014 | 238.3 | 4-2-hydroxyethyl-1-piperazineethanesulfonic acid |
| TES | 7.40 | 6.8–8.2 | −0.020 | 229.20 | 2-{[tris(hydroxymethyl)methyl]amino}ethanesulfonic acid |
| MOPS | 7.20 | 6.5–7.9 | −0.015 | 209.3 | 3-(N-morpholino)propanesulfonic acid |
| PIPES | 6.76 | 6.1–7.5 | −0.008 | 302.4 | piperazine-N,N′-bis(2-ethanesulfonic acid) |
| Cacodylate | 6.27 | 5.0–7.4 | 138.0 | dimethylarsinic acid | |
| SSC | 7.0 | 6.5-7.5 | 189.1 | saline sodium citrate | |
| MES | 6.15 | 5.5–6.7 | −0.011 | 195.2 | 2-(N-morpholino)ethanesulfonic acid |
** Values are approximate. [5]
See also
References
- ^ a b Hulanicki, A. (1987). Reactions of acids and bases in analytical chemistry. Horwood. ISBN 0853123306. (translation editor: Mary R. Masson)
- ^ Scorpio, R. (2000). Fundamentals of Acids, Bases, Buffers & Their Application to Biochemical Systems. ISBN 0787273740.
- ^ McIlvaine, T.C. (1921). "A buffer solution for colorimetric comparaison". J. Biol. Chem. 49 (1): 183–186. http://www.jbc.org/content/49/1/183.full.pdf.
- ^ Medham, J.; Denny, R.C.; Barnes, J.D.; Thomas, M (2000). Vogel's textbook of quantitative chemical analysis (5th. Ed. ed.). Harlow: Pearson Education. ISBN 0 582 22628 7. Appendix 5
- ^ "Buffer Reference Center". Sigma-Aldrich. http://www.sigmaaldrich.com/life-science/core-bioreagents/biological-buffers/learning-center/buffer-reference-center.html. Retrieved 2009-04-17.
![\beta = \frac{dn}{d(p[H^%2B])}](/2012-wikipedia_en_all_nopic_01_2012/I/45b4868896cf89177811f14f264d1d80.png)
![\frac{dn}{d(pH)}=2.303\left([H^%2B]%2B\frac{C_AK_a[H^%2B]}{\left(K_a%2B[H^%2B]\right)^2}%2B[OH^-] \right)](/2012-wikipedia_en_all_nopic_01_2012/I/05b35d6f5cdae0b5be1dadd19ba71c69.png)
![K_a = \frac{[H^%2B] [A^-]}{[HA]}](/2012-wikipedia_en_all_nopic_01_2012/I/1797ef4d5bb0d98ca3803b0932e09832.png)